

#Potential energy entangler full#
For example, the quantum phase estimation (QPE) algorithm 7 represents the natural translation of the full configuration interaction (FCI) procedure to quantum computers 8.

The direct solution to these problems on currently available quantum computer hardware is intractable. One of the most promising and immediate applications of quantum computers is solving classically intractable quantum chemistry problems 5, 6. The reason is that the solution space (i.e., the Fock space) grows factorially with the system size (e.g., the number of electrons and basis functions). Even though modern quantum many-body methods, such as density matrix renormalization group (DMRG) 2, selected configuration interaction (sCI) 3, and coupled-cluster (CC) theory 4 methods can solve larger systems, their applications are still limited to dozens of electrons and they are subject to truncation or approximations. However, since the invention of classical digital computers in the early 1940s, the exact numerical solution of this central quantum mechanical equation remains infeasible for systems roughly having more than 12 electrons distributed on 184 spin-orbitals 1. Such eigenvalues and eigenvectors can be obtained from the solution of the time-independent electronic Schrödinger equation. One of the major goals of computational chemistry is the development of methods and algorithms for the calculation of the molecular electronic ground and excited state energies and corresponding wave functions from first-principles. Proof-of-principle demonstrations are presented for several molecular systems based on quantum simulators as well as IBM quantum devices. ClusterVQE therefore allows exact simulation of the problem by using fewer qubits and shallower circuit depth at the cost of additional classical resources, making it a potential leader for quantum chemistry simulations on NISQ devices. The clusters are obtained based on mutual information reflecting maximal entanglement between qubits, whereas inter-cluster correlation is taken into account via a new “dressed” Hamiltonian. Our ClusterVQE algorithm splits the initial qubit space into clusters which are further distributed on individual (shallower) quantum circuits.

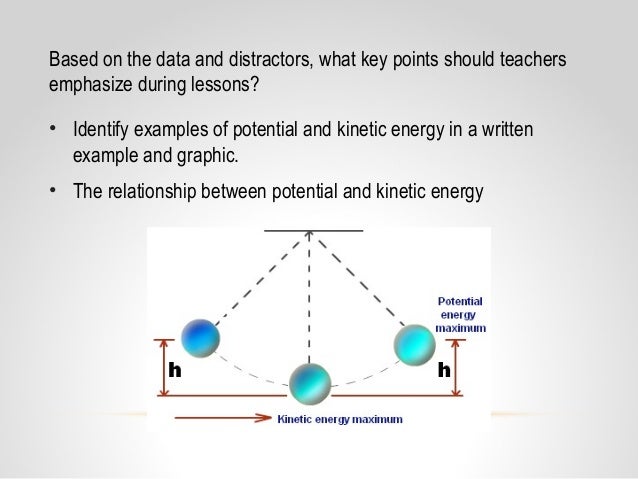
Here we present an approach to reduce quantum circuit complexity in VQE for electronic structure calculations. The practical realization is limited by the complexity of quantum circuits. `\therefore KE=TE-PE \cdots \cdots\text`).The variational quantum eigensolver (VQE) is one of the most promising algorithms to find eigenstates of a given Hamiltonian on noisy intermediate-scale quantum devices (NISQ). Total energy (TE) = Potential energy (PE) + Kinetic energy (KE) Thus by the law of energy conservation, the total energy of the bob during the oscillation remains constant which is given by, Let’s find the relation between the elevation of the bob and its kinetic energy.Ĭonsider there is no air resistance acting on the oscillating pendulum. Kinetic energy based on the elevation of bob:. Therefore the kinetic energy of the pendulum becomes maximum when the velocity of the bob becomes maximum and it becomes zero when the velocity of the bob becomes zero. For the pendulum of mass of bob ‘m’, moving with a tangential velocity of ‘v’, the kinetic energy is given by,īut as the mass of the bob is a constant quantity thus the kinetic energy of the pendulum totally depends on a velocity of a bob.


 0 kommentar(er)
0 kommentar(er)
